Quantum Secure Lightweight Cryptography with Quantum Permutation Pad
Quantum Secure Lightweight Cryptography with Quantum Permutation Pad
Volume 6, Issue 4, Page No 401-405, 2021
Author’s Name: Randy Kuanga), Dafu Lou, Alex He, Alexandre Conlon
View Affiliations
Quantropi Inc., Ottawa, K1Z 8P9, Canada
a)Author to whom correspondence should be addressed. E-mail: randy.kuang@quantropi.com
Adv. Sci. Technol. Eng. Syst. J. 6(4), 401-405 (2021); ![]() DOI: 10.25046/aj060445
DOI: 10.25046/aj060445
Keywords: AES, Quantum Permutation Gates, Quantum Permutation Pad, Permutation Matrix, Quantum Algorithm, QPP, Shannon entropy, Lightweight Cryptography, Streaming Cipher, Block Cipher
Export Citations
Quantum logic gates represent certain quantum operations to perform quantum computations. Of those quantum gates, there is a category of classical behavior gates called quantum permutation gates. As a quantum algorithm, quantum permutation pad or QPP consists of multiple quantum permutation gates to be implemented both in a quantum computing system as a quantum circuit operating on n-qubits’ states for transformations and in a classical computing system represented by a pad of n-bit permutation matrices. Since first time proposed in 2020, QPP has been recently applied to create a quantum safe lightweight block cipher by replacing SubBytes and AddRoundKey with QPP in AES called AES-QPP. In AES-QPP, QPP consists of 16 selected 8-bit permutation matrices based on the shared classical key materials. For quantum safe, the key length can be any size from 256 bits to 4 KB. That means, this QPP holds up to 4 KB of Shannon information entropy. Its code size is less than 2 KB with 4 KB of RAM memory. In this paper, we propose to apply QPP for a streaming cipher and carry out its encryption performance and the randomness analysis of this streaming cipher. The proposed QPP streaming cipher demonstrates not only good randomness in its ciphertexts but also huge performance improvement: 13x faster than AES-256, with an overall runtime space (6.8 KB).
Received: 18 June 2021, Accepted: 17 August 2021, Published Online: 28 August 2021
1. Introduction
Since the U.S. National Institute of Standards and Technology (NIST) announced the standardization of Advanced Encryption Standard or AES in 2001 [1], AES has been widely accepted as secure data encryption for data in transit or at rest. As a standard block cipher, AES accepts a fixed block size of 128 bits for three key lengths: 128, 192, and 256 bits with 10, 12, and 14 rounds respectively. Each AES round includes four steps: SubBytes, ShiftRows, MixColumns, and AddRoundKey. Over the past decade, the internet of things or IoT has captured the great attentions cross the world due to its potential to transform our daily lives through varieties of aspects such as smart home, smart city, autonomous vehicles, connected devices, etc. IoT devices are generally considered as resource constrained systems. They are often battery-powered, low computing power, and limited storages. These limitations put certain pressures on the standard AES to run in IoT devices, especially with high security requirements. The authors published their NIST report on lightweight cryptography [2], covering lightweight bloch ciphers, lightweight hash functions, lightweight message authentication codes, and lightweight streaming ciphers. In [3], the authors proposed their implementation of modified lightweight AES in FPGA, with a parallel manner for achieving better latency.
On the other hand, varieties of symmetric lightweight cryptographic algorithms have been proposed. In 2018 [4], the author have reviewed those algorithms to benchmark them on executing time, RAM memory and binary code sizes. those algorithms support the block sizes from 64 bits to 128 bits with key lengths from 80 bits to 128 bits.
AES generally faces three types of attacks: differential, linear, and integral [5]-[8]. The single static S-box representing substitutions or non-linear-transformations enables the differential analysis attacks due to some characteristic of XOR differences between input blocks and output blocks, especially impossible differences found at round 4, also called impossible differential attacks [6,7]. The differential analysis attack can be further improved with sets or multisets of input and output XOR results to create a new integral attack [8]. AddRoundKey at the end of each round contributes the linear analysis attack due to the linear transformation between rounds.
In 1994, Shor proposed an algorithm to use quantum systems or qubits to perform computations called quantum computing [9]. Shor’s algorithm enables a new natural parallel computing mechanism arising from the fundamental characteristic of their superpositions. With quantum computers, the classical exponential difficulty of prime factorizations becomes polynomial time, shaking the foundation of classical public key cryptography. The recent advancements in quantum computing development speeds up the urgency of quantum safe cryptography for both asymmetric and symmetric. In September 2019, Google announced their 54-qubit quantum computer called “Sycamore”, marked their quantum supremacy [10]. On the other hand, in [11] the author made a milestone achievement in prime factorization with D-Wave’s annealing quantum computer.
In 1996, Grover proposed his new search algorithm by using quantum computing mechanism called Grover’s algorithm [12]. Grover’s algorithm can achieve a square root complexity O( ) in the unstructured search problem of size n, while any classical algorithm needs O(n) queries. The squared searching power from the Grover’s algorithm requires any symmetric cryptography not only to double the key length from 128 bits to 256 bits, but also to be true random. For resource constrained IoT devices, standard AES cryptography itself is already heavy so the doubled key length requires extra four rounds from 10 rounds to 14 rounds. It is necessary to explore different lightweight cryptographic algorithms in the post-quantum era. In [13], the authors proposed to use quantum cryptography with One-Time-Pad or OTP for secure encryption for power grid data. This can be considered as a hybrid quantum secure encryption combining QKD with OTP. In [14], the authors proposed a new lightweight symmetric cryptographic algorithm called Saturnin by introducing two representations of AES 256-bit internal states: the 2-dimensional and 3-dimensional notations. In its 2-dimensional representation, a 256-bit state can be expressed by sixteen 16-bit registers; but in its 3-dimensional representation, it is expressed by a 4x4x4 cube of nibbles. Through those major changes, Saturnin established a new quantum resistant lightweight cryptography for 128-bit and 256-bit block ciphers and a 256-bit hash function.
Quantum mechanics allow us to have two implementations of quantum gates: physically for quantum computing power and digitally for quantum security. In [15], the authors first attempted to present classical information quantum mechanically with a state denoted by a Dirac ket over a quantum computational basis. The well-known symmetric group Sn containing entire group actions over a set of n items has its matrix representations or permutation matrices over the corresponding quantum computational basis. The extremely large size of the quantum permutation group, 28! (factorial), for an 8-qubit quantum computational basis holds huge equivalent Shannon information entropy, desirable for information security. For an 8-bit system, the permutation group is S256. Kuang and Bettenburg [15] extend the Shannon perfect secrecy of the classical one-time-pad (OTP) over GF(2n) [16], to their proposed quantum permutation pad (QPP) over a quantum computational basis. In contrast to the one-time-use nature of OTP, QPP retains the Shannon perfect secrecy over multiple uses, thanks to the general non-commutativity properties of the symmetric group.
In [17], the authors have applied QPP for a lightweight block cipher called AES-QPP, with 16 permutation matrices selected by using the shared classical random key to replace both SubBytes and AddRoundKey. AES-QPP has a footprint below 2KB and RAM memory 4KB, with performance improvement about 3x. In this paper, we extend the work [17] further for a quantum safe lightweight streaming cipher.
This paper is organized as follows: Section 2 is for the summary of lightweight block cipher AES-QPP. Then Section 3 describes the proposed streaming cipher. The randomness and performance of the proposed streaming cipher is presented in Section 4. We will draw a conclusion at the end.
2. Quantum safe Lightweight Block Cipher AES-QPP
2.1. Quantum Permutation Pad
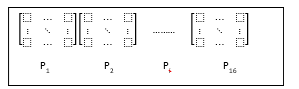
QPP is a pad of quantum permutation matrices randomly selected from the n-bit permutation group [15, 17] as shown in Fig. 1 for AES with 16 8-bit permutation matrices. They are all 28x28 square matrices and they are unitary and reversable so their reverse transformations are their transposes. This characteristic is great for lightweight cryptography, especially for resource constrained IoT devices. At the encryption side, we can use the selected QPP and then at receiving side we use their transposes or QPPT. Therefore, transformations are exactly symmetric with the same computational performance for encryption and decryption. The QPP selection is a process to map classical key materials into a QPP pad over the 8-bit computational basis. There are several algorithms to be used such as RC4 key scheduling algorithm or Fisher-Yates random shuffling algorithm. We use the Fisher-Yates algorithm to map classical key into a QPP pad as shown in Algorithm 1.
| Algorithm 1: Pseudo code of mapping a key to permutation matrix | |||
| Result: Permutation matrix P[256][256] | |||
| Input: 256 bytes of random key k[256]
Initialization: set S[256] and P[256][256] to 0 |
|||
| for i = 0 to 255 | |||
| S[i] = i; | |||
| end for
i = 255 |
|||
| while i– > 1 do | |||
| j = k[i];
swap S[j] and S[i]; |
|||
| end | |||
| for i = 0 to 255 | |||
| P[i][S[i]] = 1; | |||
| end for | |||
For each permutation matrix, we need 256 bytes of random numbers as shown in the pseudo-code. For a QPP pad with 16 permutation matrices, we would need to supply total 4 KB of random numbers. That means, the selected QPP holds total 4 KB of entropy. It is up to the desired security level to choose a right key length from 256 bits to 32,768 bits. To support this variable key length, a key scheduling is required to extend a variable key length to 4 KB.
2.2. AES-QPP
SubBytes in AES performs a substitution with a static S-box which is a 16×16 matrix. S-box can be converted to a 256×256 permutation matrix. The substitution can be considered as the permutation matrix multiplication with an 8-bit state vector over the 8-bit computational basis. AddRoundKey step performs byte-by-byte XOR operations between the output block from MixColumns step and a round key. XOR operation is a special case of permutation transformations. In our early block cipher, we use the QPP to replace both SubBytes and AddRoundKey in an AES round with the ShiftRows and MixColumns steps as follows:
- 16 8-bit QPP;
- ShiftRows;
- MixColumns;
- the same QPP as in the step
We illustrate AES-QPP in Figure 2. In standard AES, each byte in a16-byte block is supplied to the single static S-box, but in AES-QPP, each byte in a block is supplied to its corresponding permutation matrix. The last step is performed in the same way as in the first step, unlike the standard AES in the AddRoundKey step with each byte from MixColumns to be XORed with the corresponding byte in a round key. This design of AES-QPP enables us to use variable key length without change the implementation of the cryptography.
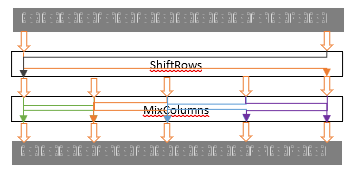 Figure 2: The proposed AES-QPP is illustrated
Figure 2: The proposed AES-QPP is illustrated
The decryption is the same process as in the encryption with transposed QPPT.
2.3. AES-QPP Rounds
In comparison with AES rounds, QPP increases the diffusion capability at least 16x with 16 permutation matrices. This extra strengthened diffusion ability helps to reduce the number of rounds. AES-256 needs 14 rounds to achieve good randomness in ciphertexts. In our early report, the number of rounds in AES-QPP was reduced to 5 rounds. The ciphertext still demonstrates excellent randomness from NIST and ENT random testing suites.
2.4. Cipher Randomness with Shannon Entropy Distribution
Cipher randomness is a good measure for a cryptosystem to avoid statistical analysis attacks. We have demonstrated randomness analysis with NIST random test suite, especially with ENT testing tool to identify any byte level and bit level biases. AES-QPP shows excellent randomness in its ciphertexts. In NIST testing suites, AES-QPP ciphers with 5 rounds pass all 15 testing cases. In the sensitive testing suite ENT, the AES-QPP ciphers not only pass 6 testing cases but also demonstrate excellent Chi Square value, arithmetic means, Monte Carlo ?, as well as serial correlation. Here we want to add analysis for Shannon entropy distribution for AES-QPP in comparison with the standard AES. Shannon entropy distribution performs analysis of each 16-bit, entropy per 16-bit random data, as well as how close to the Gaussian distribution.
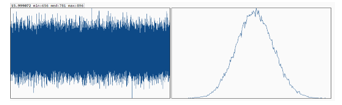
Figure 3: Shannon entropy distribution is plotted for AES-QPP-5.
Figure 3 plots the Shannon entropy distribution for AES-QPP with 5 rounds, using a 16 bits Shannon Entropy calculator [18]. . The entropy is 15.999072 per 16 bits of ciphertexts, very close to the ideal entropy 16 bits. The left side of the graph displays the frequency of each 16-bit integer. The graph displays a nice symmetric behavior around an average count. The analysis shows that the median counts are 781, minimum count 656, and maximum count 896 for 100 MB files. The right-hand side of Fig. 3 shows a good Gaussian distribution with a nice symmetric shape around the median count, indicating a good randomness in AES-QPP-5 ciphertexts.
Figure 4 plots the Shannon entropy distribution for AES-256. The same size of AES-256 ciphertext file as AES-QPP-5 is used. It demonstrates a very close relationship to Figure 5 with median counts 781, minimum counts 655 comparing with 656 in AES-QPP, and maximum counts 907, slightly better symmetry than AES-QPP. The Shannon entropy of AES-256 is 15.999087 per 16 bits of ciphertexts, extremely close to AES-QPP-5.
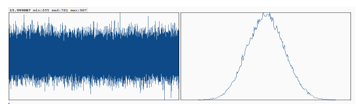 Figure 4: Shannon entropy distribution is plotted for AES-256.
Figure 4: Shannon entropy distribution is plotted for AES-256.
3. Quantum Safe Lightweight Streaming Cipher with QPP
In the last section, we discussed the block cipher implementation with QPP. We can also implement it in a streaming cipher with a pre-randomized dispatcher as shown in Figure 5.
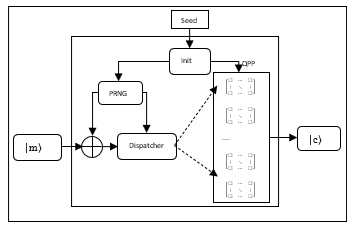 Figure 5: A streaming cipher is illustrated
Figure 5: A streaming cipher is illustrated
Seed is an input classical key material, Init box is the scheduling to map the classical key material into a QPP pad as shown in Algorithm 1. PRNG box is a pseudo random number generator used to pre-randomize input plaintexts with a directly XOR operation before dispatching them to QPP. Dispatcher box also takes a PRNG byte and performing a 4-bit right shift as an index to the permutation matrix inside the QPP pad. A ket |m⟩ represents a plaintext byte. The ciphertext denoted by a ket |c⟩ can be created byte-by-byte in the same way as input plaintexts. At the receiving side, the same shared classical key material is used to establish the same QPP pad in a transposed mode because permutation matrix is unitary and reversable. The decryption is straightforward.
QPP streaming cipher implementation eliminates the repeated rounds for better randomness ciphers, replacing with a pre-randomized process under a consideration of bijective quantum permutation transformations. We can roughly estimate the executing time for the encryption at the level of a single round AES encryption. This would dramatically improve its performance for latency and battery consumptions.
The footprint of QPP streaming cipher is about 2.5 KB, In comparison with 1.1 KB in AES-QPP because of the pre-randomization process in QPP streaming. RAM memory is the same as AES-QPP at 4KB because we still use a QPP pad with 16 permutation matrices.
4. Discussions of QPP Streaming Cipher
For the proposed QPP streaming cipher shown in Figure 5, we create a plaintext file of 120 MB by a paragraph of English sentences. Then QPP streaming encrypts the plaintext file and stores the ciphertexts into ciphertext file. The ciphertext file is passed all NIST 15 randomness test cases. We should be very interesting to see the ENT testing reports listed in Table 1, together with the results for the input plaintext file. The plaintext file comes with 4.49 bits of entropy per 8-bits, huge Chi Square value, totally wrong arithmetical mean, as well as a wrong Monte Carlo ? value. All those results show that the input plaintext file is totally biased. The ciphertext file produced from our proposed QPP streaming cipher demonstrates excellent randomness: 8 bits of entropy per 8 bits of ciphertexts, Chi Square value 237.64 with a p-value 0.775, arithmetical mean 127.49 compared to 127.50, very nice Monte Carlo ? value 3.141771788 compared to 3.14159265, and serial correlation value 8.2×10-5. The overall ENT testing results from QPP streaming cipher is very similar to AES-QPP-5 [17].
Table 1: ENT randomness testing reports for QPP streaming cipher and plaintext files of size 120 MB
| ENT | Plaintext | QPP Streaming |
| Entropy (bits) | 4.491422 | 7.999999 |
| Chi Square | 1736817422.90 | 237.64 |
| p-Value | 0.0001 | 0.775 |
| Arith. Mean | 95.7060 | 127.49 |
| Monte Carlo ? | 4.000000000 | 3.141771788 |
| Serial Corr. | 0.047905 | 0.000082 |
Figure 6 plots the Shannon Entropy distribution with 120 MB ciphertext file from a streaming encryption implementation of 16 permutation matrices. The Shannon entropy is 15.999244 bits per 16 bits of ciphertexts. The distribution demonstrates a nice Gaussian type with a med 957, minimum 826 and a maximum 1085, slightly better symmetry than AES-QPP-5 [17].
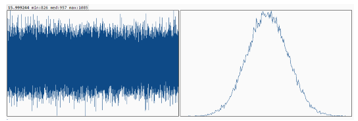 Figure 6: Shannon Entropy distribution of QPP streaming cipher: e= 15.999244, min=826, med = 957 max =1085 at 120 MB
Figure 6: Shannon Entropy distribution of QPP streaming cipher: e= 15.999244, min=826, med = 957 max =1085 at 120 MB
Table 2 illustrates performance comparisons among AES-256, AES-QPP-5, and QPP streaming cipher. For AES-256, we take the open-source implementation or Tiny-AES. AES-256 demonstrates a fastest key scheduling with 0.01 ms, then AES-QPP-5 with 0.120 ms, and QPP streaming with 0.235 ms, respectively. It is understandable that QPP initialization takes longer time because it processes 4KB key materials to select 16 permutation matrices, unlike in AES where key is only 32 bytes long. Also, in QPP streaming cipher, we take a special handling to increase confusion capability. This special handling would help to produce totally different QPP pad even with a single bit change in the supplied key materials.
Table 2: Performance comparisons are tabulated for key scheduling and encryptions for AES-256, AES-QPP-5, and QPP streaming cipher. Encryption speeds are tested with 16 bytes blocks in the same computer: MacBook Pro, 2.6 GHz 6-Core Intel Core i7.
| AES-256 | AES-QPP-5 | QPP Streaming | |
| Key Schedule | 0.01 ms | 0.120 ms | 0.235 ms |
| Encryption MB/s | 51.3 | 115.1 | 672.3 |
| Ratio | 1.0 | 2.24 | 13.1 |
| Code Footprint | 11.5 KB | 1.39 KB | 2.5 KB |
| Run Time Space | 12.0 KB | 5.39 KB | 6.5 KB |
It can also be seen from Table 2 that AES-256 is the slowest among three ciphers with an encryption speed 51.3 MB/s for 16 bytes blocks, then AES-QPP is faster than AES-256 with 115.1 MB/s, finally QPP streaming cipher is the fastest cipher with 672.3 MB/s. AES-QPP is 2.24x faster than AES-256, slightly slower than what we expected 2.8x, that may be the fact that overall permutation transformations with 16 permutation matrices take longer than each step of SubBytes and AddRoundKey in AES. However, the discrepancy is very acceptable. QPP streaming cipher is 13x faster than AES-256, indicating that pre-randomization with randomly dispatching together is almost equivalent to a single round in AES. In comparison with AES-QPP-5, QPP streaming cipher is 5x faster than AES-QPP-5.
In comparison with code sizes, compiled footprints are 11.5 KB, 1.39 KB, and 2.5 KB for AES-256, AES-QPP, and QPP streaming respectively, and runtime memory spaces are 0.47 KB for AES-256, 4 KB for both AES-QPP and QPP streaming cipher. As for overall runtime space, AES-QPP takes the least runtime space at 5.39 KB, then QPP streaming cipher at 6.5 KB, after then AES-256 needs the most runtime space at 12 KB.
5. Conclusion
We have applied quantum permutation pad or QPP to establish both lightweight quantum safe block cipher and streaming cipher. In a block cipher implementation, QPP replaces both SubBytes and AddRoundKey in a standard AES or called AES-QPP. In addition to cipher randomness analysis in [17], we perform the Shannon entropy distribution for a more complete randomness analysis of this quantum safe block cipher.
In this paper We explored the QPP algorithm for a streaming cipher with a straightforward pre-randomization and random distribution process. The randomness analysis of the QPP streaming cipher demonstrates very good randomness, especially with ENT randomness testing tool. The very promising encryption speed plus overall memory space makes QPP streaming be a good candidate for quantum safe lightweight streaming cipher and AES-QPP for quantum safe lightweight block cipher.
In the future, we may extend the exploration both ciphers for 4-bit permutation matrix pad to further reduce their runtime memory spaces.
Conflict of Interest
The authors declare no conflict of interest.
- Information Technology Laboratory (National Institute of Standards and Technology), Announcing the ADVANCED ENCRYPTION STANDARD (AES), Computer Security Division, Information Technology Laboratory, National Institute of Standards and Technology Gaithersburg, MD 2001.
- K. McKay, L. Bassham, M. Sonmez, N. Mouha, Report on Lightweight Cryptography, NIST Interagency/Internal Report (NISTIR), National Institute of Standards and Technology, Gaithersburg, MD, [online], 2017, doi:10.6028/NIST.IR.8114 (Accessed August 23, 2021).
- M. James, D. S. Kumar, “An Implementation of Modified Lightweight Advanced Encryption Standard in FPGA?” Procedia Technology, 25, 582-589?2016, doi:10.1016/ j.protcy.2016.08.148.
- D. Dinu, Y. L. Corre, D. Khovratovich, L. Perrin, J. Großschädl, A. Biryukov, “Triathlon of lightweight block ciphers for the Internet of things,” Journal of Cryptographic Engineering, 9 (3), 283–302, 2018, doi:10.1007/s13389-018-0193-x. S2CID 1578215.
- J. Daemen, V. Rijmen, The Design of Rijndael, AES – The Advanced. Encryption Standard, Springer-Verlag 2002.
- H. M. Heys, S. E. Tavares, “Substitution-permutation networks resistant to differential and linear cryptanalysis,” J. Cryptology 9, 1–19, 1996. doi:10.1007/BF02254789.
- L. O’Connor, On the distribution of characteristics in bijective mappings, J. Cryptology 8, 67–86, 1995, doi:10.1007/ BF00190756.
- J. Lu, O. Dunkelman, N. Keller, J. Kim, “New Impossible Differential Attacks on AES,” In: Chowdhury D.R., Rijmen V., Das A. (eds) Progress in Cryptology – INDOCRYPT 2008. INDOCRYPT 2008. Lecture Notes in Computer Science, 5365, Springer, Berlin, Heidelberg. doi?10.1007/978-3-540-89754-5_22.
- K. Autre, K. Arya, , et al? “Quantum supremacy using a programmable superconducting processor?” Nature 574 (7779)?505–510. 2019.
- P. W. Shor, “Algorithms for quantum computation: discrete logarithms and factoring?” in Proceedings 35th Annual Symposium on Foundations of Computer Science, IEEE Comput. Soc. Press: 124–134, 1994.
- B. Wang, F. Hu, H. Yao, et al., “Prime factorization algorithm based on parameter optimization of Ising model,” Sci Rep 10, 7106, 2020, doi:10.1038/s41598-020-62802-5
- L. Grover, “A fast quantum mechanical algorithm for database search,” In: Proceedings of the 28th ACM STOC, Philadelphia, Pennsylvania, 212–219, ACM Press, 1996.
- Y. Li, P. Zhang and R. Huang, “Lightweight Quantum Encryption for Secure Transmission of Power Data in Smart Grid,” in IEEE Access, 7, 36285-36293, 2019, doi: 10.1109/ACCESS.2019.2893056.
- A. Canteaut, S. Duval, G. Leurent, M. Naya-Plasencia, L. Perrin, T. Pornin, A. Schrottenloher, “Saturnin: a suite of lightweight symmetric algorithms for post-quantum security,” IACR Transactions on Symmetric Cryptology, 2020(S1), 160-207, doi:10.13154/tosc.v2020.iS1.
- R. Kuang, N. Bettenburg, “Shannon Perfect Secrecy in a Discrete Hilbert Space,” 2020 IEEE International Conference on Quantum Computing and Engineering (QCE), Denver, CO, USA, 249-255, 2020, doi: 10.1109/QCE49297.2020.00039.
- C. E. Shannon, “Communication Theory of Secrecy Systems?” Bell System Technical Journal? 28 (4): 656–715? October 1949.
- R. Kuang, D. Lou, A. He and A. Conlon, “Quantum Safe Lightweight Cryptography with Quantum Permutation Pad,” 2021 IEEE 6th International Conference on Computer and Communication Systems (ICCCS), 790-795, 2021, doi: 10.1109/ICCCS52626.2021.9449247.
- Server Test, https://servertest.online/entropy.